Hai sobat, kamu sering dong bolak-balik dari dapur atau bahkan sering melihat benda-benda yang menjadi contoh untuk kita dalam pelajaran. Nah, kali ini kita akan belajar matematika dengan menggunakan benda yang ada di dapur seperti gelas, tabung elpiji dan lain sebagainya yang merupakan bangun ruang yah….
Disini yang akan kita pelajari ialah rumus untuk mencari volume dan juga rumus lias permukaan dari tabung. Sebelumnya apakah kamu tahu tabung itu apa sih dalam matematika?
Tabung ialah suatu bangun ruang dengan alas dan tutup yang bentuknya lingkaran. Selain itu tabung juga memiliki selimut yang lengkung berasal dari persegi panjang.
[ez-toc]
Rumus Volume Tabung
Kamu harus ingat yah tabung itu memiliki alas dan tutup yang bentuknya lingkaran. Untuk menghitung volume tabung kita harus menghitung tinggi dan luas alas dari tabung. Bagaimana sih cara menghitungnya dan rumusnya bagaimana? Tadi kan sudah dikatakan bahwa kunci utama ada pada tinggi dan luas alasnya, berikut ini adalah rumus volume tabung yang dapat kita pakai:

Rumus Luas Permukaan Tabung
Luas permukaan tabung merupakan jumalah keseluruhan dari sisi- sisi tabung. Bidang pembentuk dari tabung sama dengan jumlah dari sisi-sisi tabung. Bidang pembentuk tabung terdiri dari 3 yaitu 2 lingkaran sebagai tutup dan alas serta 1 sebagai selimut yang bentuknya persegi panjang.
Luas permukaan dari tabung sangat mempengaruhi ukuran dari tabung, berukuran kecil atau besar. Makanya ada ukuran gelas maupun gas yang bermacam-macam.
Ukuran dari benda tersebut dapat diperhitungkan berapa banyak volume yang dapat diisi. Nah, Coba perhatikan luas permukaan dari tabung dibawah ini:
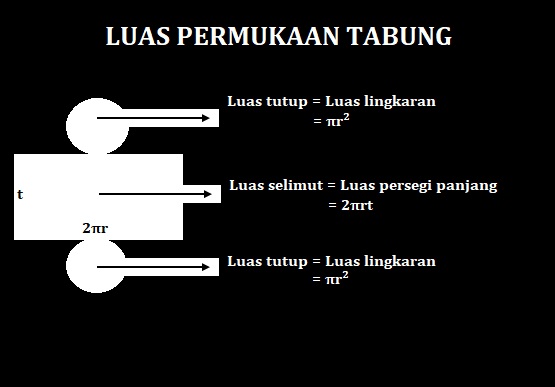
Nah, agar lebih jelas dibawah ini adalah rumus untuk menghitung luas permukaan tabung:

Contoh Soal dan Pembahasannya
Untuk melatih apakah kamu sudah mengetahui bagaimana cara menggunakan dan menghitung rumus volume dan luas permukaan tabung dengan benar dan tepat dibawah ini ada soal-soal beserta pembahasannya.
Contoh Soal 1:
Hitunglah volume dari sebuah tabung yang mempunyai diameter 28 cm dan tinggi 20 cm?
Jawab:
diameter (d)= 28 cm, karena r = 1/2 d maka r = 14 cm
tinggi (t)= 20 cm
Volume Tabung = πr²t
= (22/7) x 14 cm² x 20 cm
= (22/7) x 14 cm x 14 cm x 20 cm
= (22/7) x 3.920
= 12.320 cm³
Jadi, volume tabung tersebut adalah 12.320 cm³
Contoh Soal 2:
Seorang pekerja infrastruktur memotong sebuah kayu dan membentuknya seperti tabung yang memiliki luas alas yaitu 50 cm². Tabung tersebut mempunyai tinggi 21 cm. Berapakah volume tabung itu?
Jawab:
Volume tabung = πr²t atau
- V = luas alas (luas lingkaran) x tinggi
- V = 50 cm² x 21 cm
- V = 1050 cm³
Jadi, volume tabung dari kayu tersebut adlah 1050 cm³
Contoh Soal 3:
Sebuah tabung dengan diameter 18 cm dan tinggi 10 cm. Hitunglah berapa luas permukaan yang dari tabung tersebut?
Jawab:
- Lp = 2πr(r + t)
- = 3,14 x 9 (9 + 10)
- = 3,14 x 171
- = 536,94
Jadi, luas permukaan tabung tersebut adalah 536,94 cm²
Contoh Soal 4:
Jika sebuah tabung mempunyai jari-jari (r) = 7 cm dan tinggi (t) 15 cm. Hitunglah berapa luas selimut dari tabung itu !
Jawab:
- Luas selimut = 2πrt
- = 2 × 22/7 × 7 × 15
- = 44 × 15
- = 660
Jadi, Luas selimut dari tabung tersebut adalah 660 cm²
Contoh Soal 5:
Sebuah tabung mempunyai jari-jari alas = 12,5 cm dan tinggi = 20 cm. Hitunglah berapa: (a) Luas selimut dari tabung; (b) Luas tabung tanpa tutup; serta (c) Luas tabung seluruhnya
Diketahui:
r = 12,5 cm; t = 20 cm; π = 3,14
Jawab:
a. Luas selimut
- = 2πrt
- = 2 × 3,14 × 12,5 cm × 20 cm
- = 1570 cm²
b. Luas selimut tanpa tutup
- = πr² + 2πrt
- = (3,14 × 12,5 cm × 12,5 cm) + ( 2 × 3,14 × 12,5 cm × 20 cm)
- = 490,625 + 1.570
- = 2060,625 cm²
c. Luas tabung seluruhnya
- = 2πr (r + t)
- = 2 × 3,14 × 12,5 cm × (12,5 cm + 20 cm)
- = 2551,25 cm²
Jadi, luas selimut tabung ialah 1570 cm²; luas selimut tanpa tutup 2060,6 cm²; da luas dari tabung seluruhnya ialah 2551,25 cm²
Contoh Soal 6:
Sebuah tabung mempunyai luas selimut namun tanpa tutup yakni 628 cm². Sedangkan tinggi dari tabung tersebut 10 cm nilia phi yang harus digunakan ialah π = 3,14. Tentukanlah berapa luas tabung itu ?
Diketahui: luas selimut tanpa tutup = 628 cm²; t = 10 cm; π = 3,14
Jawab:
Luas selimut dari tabung = 628 cm²
2πrt = 628
2 × 3,14 × r × 10 = 628
62,8 r = 628
r = 10 cm
Luas tabung
- = πr² + 2πrt
- = (3,14 × 10 cm x 10 cm) + (2 × 3,14 × 10 cm × 10 cm)
- = 314 cm² + 628 cm²
- = 942 cm²
Jadi, luas tabung tanpa tutup tersebut adalah 942 cm²
Contoh Soal 7:
Hitunglah berapa jari-jari dari sebuah tabung dengan tinggi 4 cm serta luas selimut 162 cm²!
Diketahui:
t = 4 cm; Ls = 162 cm²; π = 3,14
Jawab:
- r = Ls / (2 x π x t)
- r = 162 cm² / (2 x 3,14 x 4 cm)
- r = 162 cm² / 25,12 cm
- r = 6,449 cm
Jadi, nilai jari jarinya adalah 6,5 cm
Contoh Soal 8:
Diketahui sebuah tabung memiliki r = 7 cm dan tinggi yaitu 28 cm. Hitunglah berapa volume tabung, berapakah luas permukaannya, berapa luas selimut, serta berapa luas alas tanpa tutup !
Jawab:
a. Volume tabung
- V = πr²t
- V = (22/7) x 7 cm x 7 cm x 28 cm
- V = 4312 cm³
b. Luas permukaan
- Lp = 2πr (r+ t)
- Lp = 2 x (22/7) x 7 cm x (7 cm + 28 cm)
- Lp = 1540 cm²
c. Luas selimut
- Ls = 2πrt
- Ls = 2x (22/7) x 7 cm x 28 cm
- Ls = 1232 cm²
d. Luas permukaan tabung tanpa tutup
- L tanpa tutup = La + Ls
- L tanpa tutup = πr² + 2πrt
- L tanpa tutup = (22/7 x 7 cm x 7 cm) + 1232 cm²
- L tanpa tutup = 154 cm² + 1232 cm²
- L tanpa tutup = 1386 cm²
Jadi, volume tabung adalah 4312 cm³, berapakah luas permukaannya ialah 1540 cm², berapa luas selimut adalah 1232 cm², serta berapa luas alas tanpa tutup adalah 1386 cm².
Nah, dari semua soal-soal beserta pembahasannya diatas kamu harus bisa menggali lagi kemampuanmu dalam menyelesaikan berbagai macam soal-soal yang berhubungan dengan bangun ruang terutama tabung yah, Agar lebih mudah menyelesaikan soalnya kamu terlebih dahulu harus memahami atau menghapal rumus-rumus volume tabung diatas yah. Terimakasih, semoga bermanfaat…
Editor: Muchammad Zakaria
Download berbagai jenis aplikasi terbaru, mulai dari aplikasi windows, android, driver dan sistem operasi secara gratis hanya di Nesabamedia.com:
A woman who struggles to live happily with her family without others knowing her social status







