Rumus Trigonometri : Contoh Soal & Pembahasannya [LENGKAP]

Bagi Anda yang masih menjadi seorang pelajar maupun yang sudah bekerja pasti pernah belajar pelajaran matematika. Mata pelajaran satu ini memang sudah di ajarkan kepada siswa sejak masa sekolah dasar hingga siswa yang ada di universitas.

Bahkan mata pelajaran matematika selalu dimasukkan ke dalam ujian sekolah maupun ujian nasional di beberapa tingkat pendidikan.

Karena mata pelajaran satu ini juga banyak siswa yang sering mengeluh ketika sedang mendapatkan tugas untuk mengerjakan soal matematika. Memang beberapa rumus yang ada di mata pelajaran matematika cukup menguras pikiran untuk di mengerti. Salah satu rumus matematika yang cukup sulit untuk dipelajari adalah rumus trigonometri.

[ez-toc]

Kumpulan Rumus Trigonometri

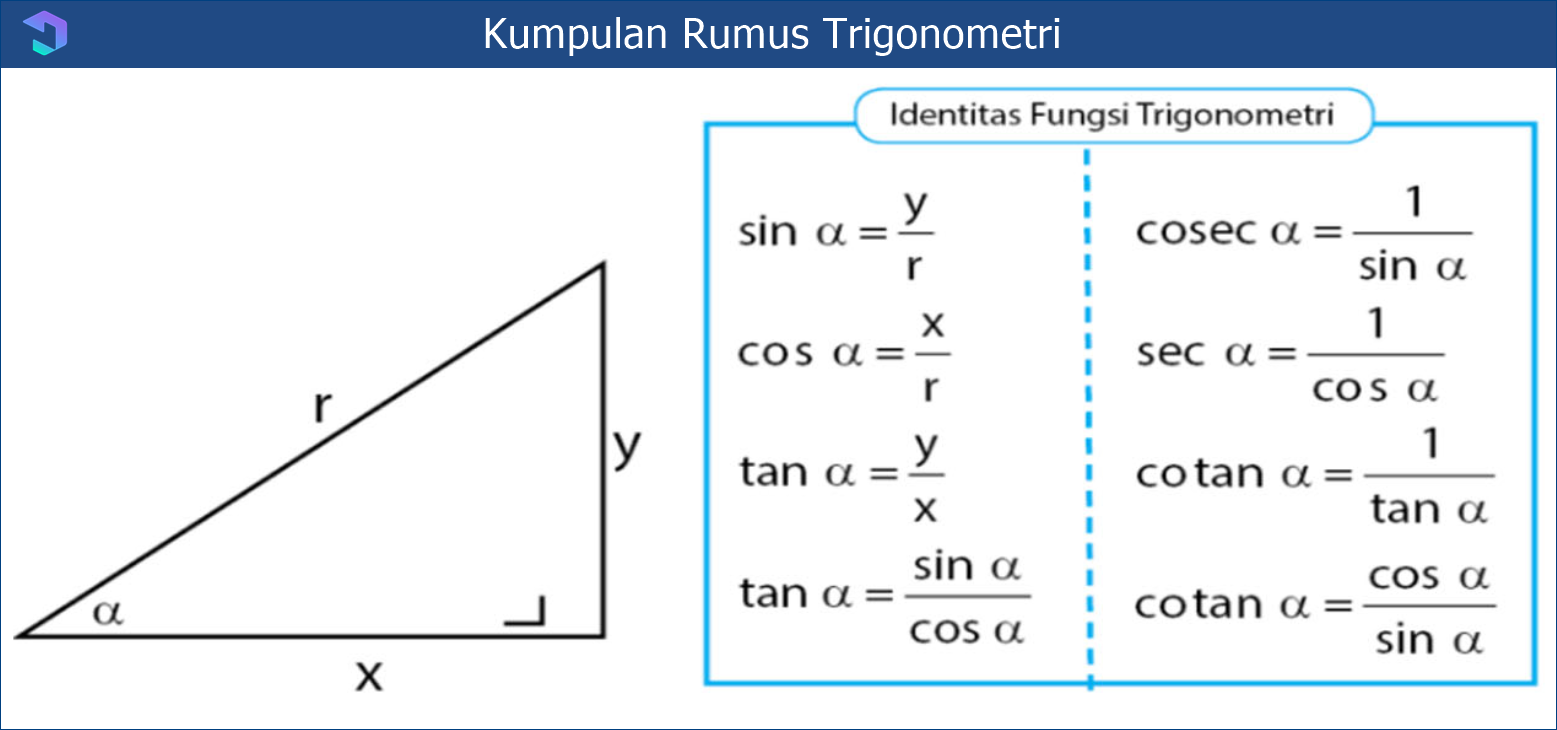
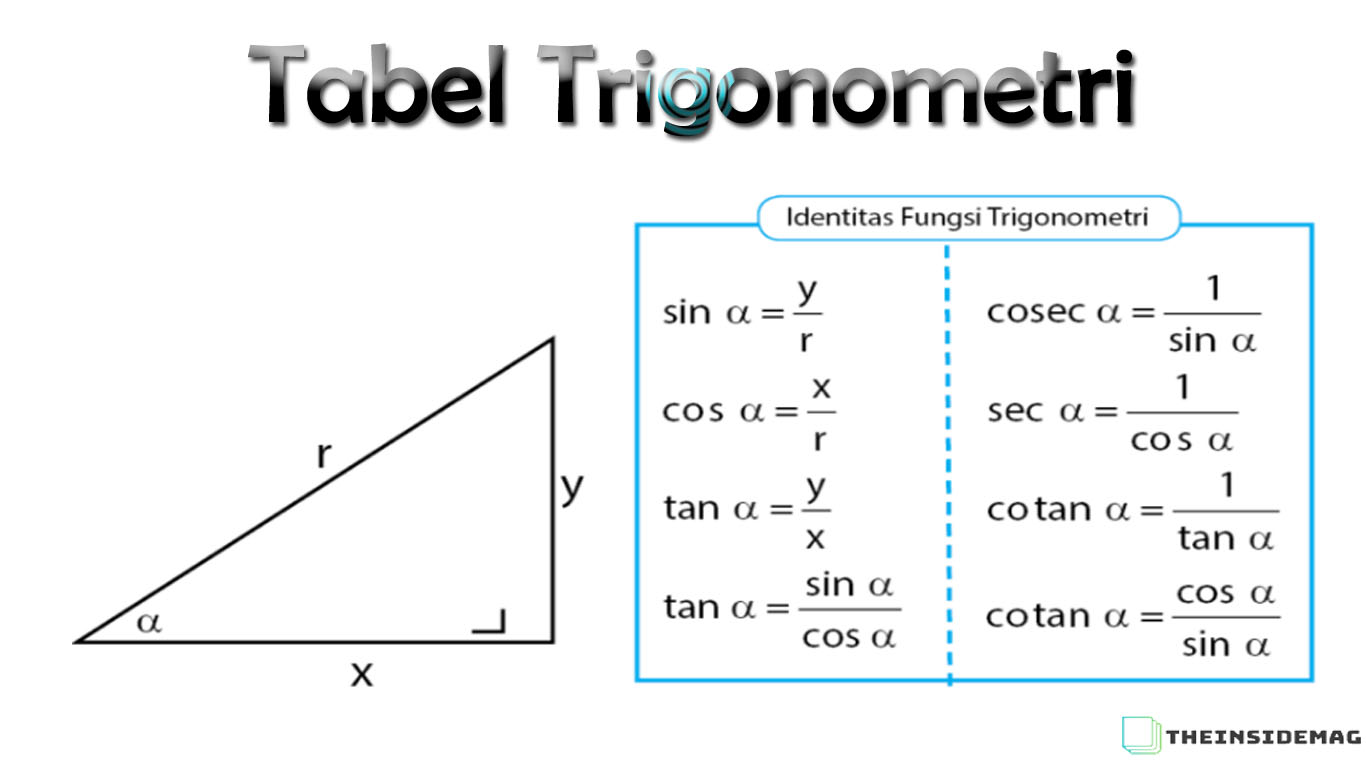
Berbicara tentang rumus trigonometri maka Anda akan mempelajari tentang bentuk segitiga. Karena rumus trigonometri merupakan sebuah rumus yang mempelajari tentang hubungan antara sudut dan sisi yang ada pada bangun segitiga. Sedangkan fungsi trigonometri sendiri dibagi menjadi tiga, yaitu fungsi consinus (cos), sinus (sin), secan (sec), tangen (tan), cotangen (cotan), dan cosecan (cosec).

1. Rumus Fungsi Trigonometri

Rumus trigonometri yang pertama berasal dari fungsi-fungsi trigonometri diatas. Dimana setiap rumus memiliki cara perhitungan dari setiap sudut segitiga. Adapun rumus fungsi trigonometri adalah

Untuk rumus sin α digunakan untuk menghitung sisi depan yang dibagi dengan sisi miring. Sedangkan rumus cos α digunakan menghitung sisi samping dibagi sisi miring. Dan tan α merupakan rumus dari sisi depan di bagi sisi miring dalam segitiga. Guna mempermudah mengingat ketiga rumus fungsi diatas maka Anda bisa memakai singkatan berikut ini.

SinDeMi

Singkatan dari Sinus Depan Miring atau rumus sin α.

CosSaMi

Cosinus Samping Miring atau rumus cos α.

TanDeSa

Dan singkatan TanDeSa kepanjangan dari Tangen Depan Samping atau rumus tan α.

2. Rumus Identitas Trigonometri

Rumus identitas trigonometri merupakan rumus yang membandingkan trigonometri dengan variabel sudut x. Dimana variabel x ini di dapat dari ukuran derajat dan radian. Sedangkan cara untuk menyelesaikan persamaan sin xº = sin ?° (x ? R) adalah:

Pertama gunakan perbandingan sudut sin (180º – ?º) = sin ?º dan sin (?º + k.360º) = sin ?º. Kemudian masukkan ke dalam persamaan sin xº = sin ?º menjadi

Jika sin x⁰ = sin ?⁰ (x ? R), maka:

x = ? + k.360⁰ atau x = (180⁰ ? ?) + k.360, dengan k ? B

Catatan: x ada dalam derajat

Jika sin x = sin A (x ? R), maka:

x = A + k.2? atau x = (? ? A) + k.2?, dengan k ? B

Catatan: x ada dalam radian

3. Rumus Jumlah dan Selisih Sudut Trigonometri

Rumus yang ketiga dalam trigonometri adalah rumus jumlah dan selisih sudut trigonometri. Adapun rumusnya adalah:

Rumus ini digunakan untuk menjumlahkan sudut dan sisi yang ada di bangun segitiga.

4. Rumus Perkalian Trigonometri

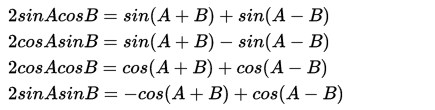
Sedangkan untuk perkalian di sudut dan sisi pada bangun segitiga maka Anda bisa memakai rumus perkalian trigonometri diatas.

5. Rumus Jumlah dan Selisih Trigonometri

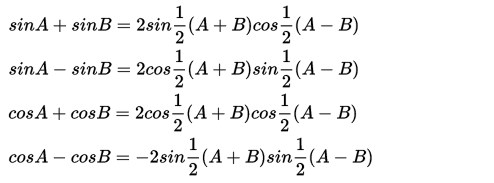
Dalam segitiga tidak hanya ada rumus penjumlahan saja namun juga ada sisi yang harus di jumlah sekaligus di cari selisihnya dengan rumus jumlah dan selisih trigonometri diatas.

6. Rumus Sudut Rangkap 2 dan 3 Trigonometri

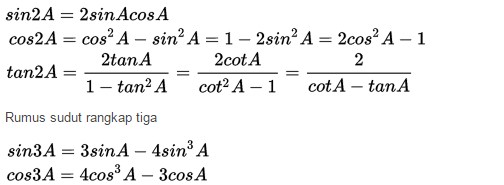Jika Anda menemukan soal sudut rangkap 2 dan 3 dari segitiga maka gunakan rumus sudut rangkap 2 dan 3 pada trigonometri.

7. Rumus Setengah Sudut Trigonometri

Sudut yang bisa dihitung pada segitiga tidak hanya sudut penuh saja tetapi setengah sudut segitiga bisa dihitung dengan rumus setengah sudut trigonometri diatas.

8. Rumus Sudut Istimewa Trigonometri

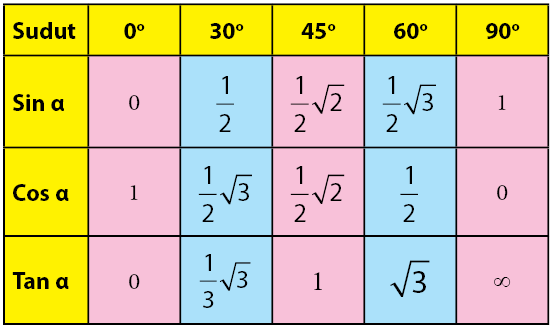
Selain ketujuh rumus diatas, pada rumus trigonometri juga terdapat sudut istimewa yaitu $0^{o}$ , $30^{o}$ , $45^{o}$ , $60^{o}$ , dan $90^{o}$ . Dimana untuk setiap rumus sudut istimewa trigonometri bisa Anda lihat pada grafik diatas. Sedangkan untuk rumus mencari nilai trigonometri yang ada hubungannya dengan sudut istimewa diatas maka gunakan rumus berikut ini.

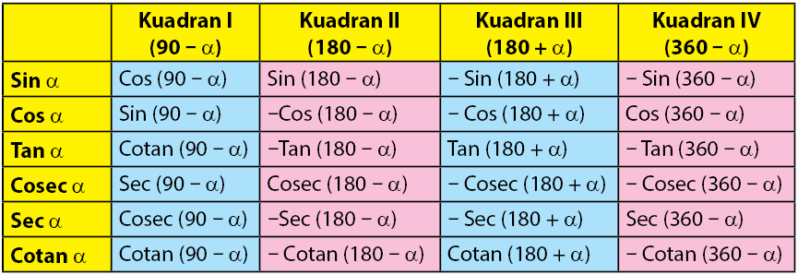
Jadi ketika Anda sedang mengerjakan sebuah soal trigonometri maka Anda harus mencari tahu terlebih dahulu apakah soal tersebut soal dengan rumus trigonometri biasa atau dengan rumus soal trigonometri istimewa. Sebab setiap rumus yang Anda gunakan akan memberikan hasil yang berbeda begitupun dengan ketepatan dalam menjawab soal.

Contoh Soal Trigonometri

Rumus Trigonometri dan Contoh Soalnya

Bagaimana? Apakah Anda sudah mengerti tentang rumus trigonometri diatas? Memang rumusnya cukup sulit untuk di pahami namun bukan berarti Anda tidak bisa jika terus mencoba. Anda juga bisa memahami rumus-rumus trigonometri melalui soal-soal trigonometri. Adapun beberapa contoh soal mengenai trigonometri yang bisa Anda coba adalah:

1. Tentukan nilai dari sin 105º + sin 15º

Soal trigonometri diatas merupakan soal trigonometri tipe penjumlahan sehingga Anda bisa memakai rumus trigonometri penjumlahan yaitu 2 sin ½ (A+B) cos ½ (A-B). Cara pengerjaannya adalah:

nilai dari sin 105° + sin 15° = 2 sin ½ (105+15)°cos ½ (105-15)°
= 2 sin ½ (102)° cos ½ (90)°
= sin 60° cos 45°

Jadi jawaban dari soal sin 105º + sin 15º adalah sin 60º cos 45º.

2. Tentukan nilai persamaan dari sin xº sin 25º

Penyelesaian soal diatas yaitu:

x = 25⁰ + k.360⁰ atau x = (180⁰ ? 25⁰) + k.360⁰

= 155⁰ + k.360⁰

Jadi, x = 25⁰ + k.360⁰ atau 155º + k.360⁰

Jadi nilai persamaan dari sin xº sin 25º adalah x = 25⁰ + k.360⁰ atau 155º + k.360^0.

3. Tentukan nilai dari perkalian 2 cos 75º cos 15º

Soal yang ketiga diatas model soal perkalian trigonometri. Rumus yang digunakan yaitu 2 cos A cos B = cos (A+B) + cos (A-B). Penyelesaian soalnya adalah:

2 cos 75° cos 15° = cos (75 +15)° + cos (75 – 15)°
= cos 90° + cos 60°
= 0 + ½
= ½

Jadi hasil dari perkalian 2 cos 75º cos 15º adalah ½.

4. Sebuah segitiga ABC sudut lancip, diketahui cos A = 4/5 dan sin B =12/ 13 , maka sin C adalah…

Karena segitiga ABC memiliki sudut lancip , maka sudut A,B dan C juga lancip, jadi :

cos A = 4/5, maka sin A = 3/5,
sin B = 12/13, maka cos B = 5/13
A + B + C = 180°, (jumlah sudut -sudut dalam satu segitiga = 180)
A + B = 180 – C
sin (A + B) = sin (180 – C)
sin A . cos B + cos A.sin B = sin C, (sudut segitiga yang saling berelasi : sin(180-x) = sin x)
sin C = sin A.cos B + cos A.sin B
sin C = 3/5.5/13 + 4/5.12/13
sin C = 15/65 + 48/65 = 63/65

Dari rumus diatas maka sin C nilainya adalah 63/65

5. Tentukan nilai dari sin 120^o

Untuk soal nomor 5 ini ada dua cara pengerjaannya. Cara yang pertama yaitu:

120 = 90 + 30

Sehingga sin 120^o dapat dihitung dengan rumus Sin 120^o = Sin (90^o + 30^o) = Cos 30^o (didapat nilai positif sebab 120º ada di kuadran II (2), jadi hasilnya juga positif)
Cos 30^o = ½ √3

Atau dengan cara kedua, yaitu:

Sama seperti 180^o-80^º

Sin 120^o = Sin (180^o – 60^o) = sin 60^o = ½ √3

Jadi hasil dari sin 120º adalah ½ √3.

6. Sebuah segitiga ABC mempunyai panjang sisi AB=6 cm ,BC=8 cm AC=7 cm. Nilai dari cos A adalah..

Cara mengerjakan soal diatas adalah dengan rumus:

Cos A=(AB²+AC²-BC²)/2(AB . AC)
Cos A=6²+7²-8²/2(6 . 7)
Cos A = 36+49-64/2(42)
Cos A=21/84

Sehingga ditemukan nilai cos A yaitu 21/84.

7. Titik P dan Q dinyatakan menggunakan kordinat polar. Maka tentukan jarak antar titik P dan Q!

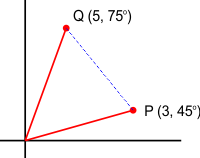
Soal Trigonometri 7

Untuk soal diatas maka gunakan rumus consinus, yaitu:

Besar sudut POQ = 180^o – (75^o+45^o) = 60^o.
PQ² = OQ² + OP² – 2.OQ.OP cos ∠POQ
PQ² = 3² + 5² – 2.3.5 cos 60^o c
PQ² = 9 + 25 – 30. 0,5
PQ² = 9 + 25 -15
PQ² = 19
PQ = √19 = 4,36