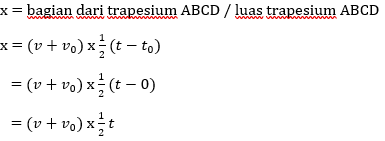Kita pasti sudah tidak asing lagi mendengar singkatan GLBB dan GLB. Yap! keduanya merupakan materi yang kita pelajari di bangku sekolah pada mata pelajaran fisika. Dimana GLBB adalah Gerak Lurus Berubah Beraturan dan GLB adalah Gerak Lurus Beraturan.
Dalam kehidupan sehari-hari penerapan keduanya juga sudah kita alami seperti pada saat kita bersepeda di jalan menurun, ternyata hal ini merupakan salah satu contoh GLBB dan ketika sebuah kereta api melaju dengan kecepatan konstan yang merupakan salah satu contoh GLB.
Artikel ini akan membahas tentang rumus GLBB dan GLB lengkap dengan contoh soal dan pembahasannya. Berikut penjabarannya!
[ez-toc]
Rumus GLBB
Jika perubahan kecepatan benda terjadi secara teratur dan lintasan yang dilalui merupakan lintasan lurus, maka gerak benda tersebut dinamakan “gerak lurus berubah beraturan”.
Karena perubahan kecepatan yang dialami benda teratur, dengan kata lain, gerak lurus berubah beraturan adalah gerak pada lintasan lurus dengan percepatan tetap. Dari hubungan kecepatan dan percepatan ini, kita dapat menurunkan rumus kecepatan gerak lurus berubah beraturan, yaitu sebagai berikut.
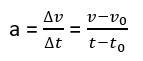
dengan mengambil t0 = 0, maka :
Keterangan :
v = kecepatan akhir
v0= kecepatan awal
a = percepatan (tetap)
t = waktu yang ditempuh
Selain itu kita juga dapat menentukan persamaan perpindahan (x) gerak lurus berubah beraturan berdasarkan grafik berikut ini.
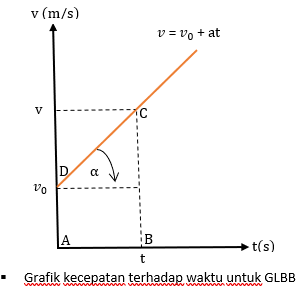
Karena v=v0+ at, maka :
Persamaan untuk kasus yang lebih umum, dimana x0 =perpindahan/posisi awal.
Sehingga grafik perpindahan terhadap waktu dapat kita gambarkan sebagai berikut.
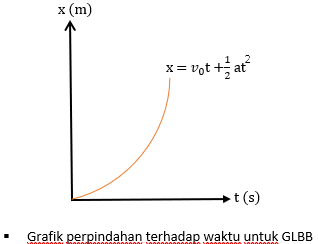
Nah, berdasarkan persamaan x = x0 + v0t + 1/2 at2 dan v=v0+ at, kita dapat menentukan hubungan antara kecepatan,percepatan, dan perpindahan untuk GLBB sebagai berikut.
Jika perpindahan awalnya, x0 = 0, maka :
Rumus GLB
Ketika sebuah benda menempuh jarak yang sama dalam selang waktu yang sama melalui sebuah lintasan yang lurus, maka gerak benda ini disebut “gerak lurus beraturan”. Dalam hal ini benda memiliki kecepatan (laju) tetap, maka percepatannya nol.
Dengan begitu untuk mencari jaraknya, dapat dirumuskan sebagai berikut :
s = v x t
Keterangan :
s : jarak (m atau km)
v : kecepatan (m/s atau km/jam)
t : waktu ( sekon atau jam)
Dengan begitu grafik kecepatan terhadap waktu dari gerak ini berupa garis lurus horizontal seperti berikut ini.
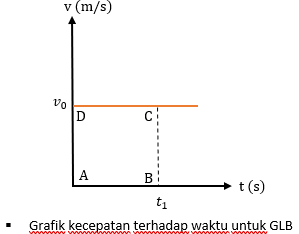
Maka perpindahannya dapat dirumuskan dengan luas area ABCD, yaitu :
x = (t1-0) x (v0– 0)
Dengan mengambil nilai t1-0=t dan v0– 0=v, maka :
x = v x t
Keterangan :
x = perpindahan/posisi benda (m atau km)
v = kecepatan (m/s atau km/jam)
t = waktu tempuh (sekon atau jam)
Dari rumus tersebut diatas dapat kita ketahui bahwa pada gerak lurus beraturan jarak dan perpindahan benda sama, dimana s = v x t dan x = v x t.Â
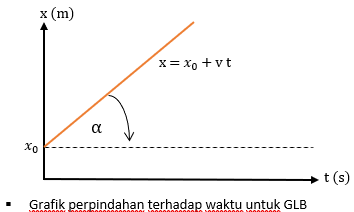
Sementara grafik perpindahan terhadap waktu untuk gerak ini dimana x0 merupakan posisi awal, yaitu sebagai berikut.
Contoh Soal GLBB dan GLB dan Pembahasan
1. Sebuah mobil bergerak lurus beraturan dengan kecepatan tetap 50 km/jam. Berapakah jarak yang ditempuh mobil setelah 5 jam ?
Pembahasan :
v = 50 km/jam
t = 5 jam
Dijawab :
s = v x t
s = 50 km/jam x 5 jam
s = 250 km
Jadi, jarak yang ditempuh mobil setelah 5 jam adalah 250 km.
2. Kereta api yang bergerak lurus beraturan dapat menempuh jarak 35 m selama 0,05 sekon. Berapakah kecepatan kereta api tersebut ?
Pembahasan :
s = 35 m
t = 0,05 s
Dijawab :
v= s/t
v = 35 m / 0,05 s
v = 700 m/s
Jadi, kecepatan kereta api tersebut adalah 700 m/s
3. Perpindahan awal suatu benda yang bergerak dengan kecepatan tetap 6 m/s adalah -12 m. Kapan benda tersebut mencapai titik dengan perpindahan 12 m?
Pembahasan :
x = 12 m
x0Â = -12m
v = 6 m/s
Dijawab :
x = x0+ v x t
12 m/s = -12 m/s + 6 t
6 t = 12 m/s + 12 m/s
t = 24 m/s : 6 s
t = 4 s
Jadi, benda tersebut mencapai titik dengan perpindahan 12 m/s adalah dalam waktu 4 s.
4. Miyako berada 40 m dari gerbang sekolah. Ia mengendarai motor dengan kecepatan 30 m/s menjauhi gerbang sekolah dalam waktu 50 sekon. Hitung posisi akhir Miyako dan jarak yang ditempuh Miyako !
Pembahasan :
x0 = 40 m
v = 30 m/s
t = 50 s
Dijawab :
x = x0 + v t
x = 40 m + (30 m/s x 50 s)
x = 40 m + 1.500 m
x = 1.540 m
Maka, jarak yang ditempuh Miyako adalah s = x – x0 = 1.540 m – 40 m = 1.500m atau s = v x t = 30 m/s x 50 s = 1.500 m.
5. Sebuah mobil bergerak lurus beraturan dengan kecepatan tetap 40 m/s selama 30 sekon. Berapa jarak yang ditempuh mobil selama waktu tersebut ?
Pembahasan :
x0 = 0
v = 40 m/s
t = 30 s
Dijawab :
x = x0 + v t
x = 0 + (40 m/s x 30 s)
x = 1.200 m
Jarak yang ditempuh dapat kita cari dengan rumus s = x – x0 = 1.200 m – 0 = 1.200 m.
Nah, dari hal tersebut diatas dapat membuktikan bahwa pada gerak lurus beraturan, jarak dan perpindahan memiliki nilai yang sama.
6. Sebuah mobil bergerak lurus dipercepat beraturan dengan kecepatan awal 35 m/s. Setelah 15 sekon, kecepatannya menjadi 50 m/s. Hitunglah percepatannya ! (t0=0)
Pembahasan :
v0Â = 35 m/s
t0 = 0
v = 50 m/s
t = 15 s
Dijawab :
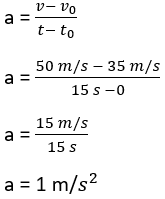
7. Sebuah partikel bergerak dengan percepatan tetap sebesar 4 m/s2. Setelah bergerak selama 8 sekon, kecepatan partikel tersebut menjadi 400 m/s. Tentukan kecepatan awal partikel tersebut !
Pembahasan :
a = 4 m/s2
t = 8 s
v0Â = 400 m/s
Dijawab :
v= v0+ at
400 m/s = v0 + (4 m/s2Â x 8 s)
400 m/s = v0 + 32 m/s
v0 = 400 m/s – 32 m/s
v0 = 368 m/s
8. Sebuah benda bergerak dengan kecepatan awal 2 m/s. Setelah bergerak selama 8 sekon, kecepatan benda tersebut menjadi 10 m/s. Berapakah perpindahan yang ditempuh benda selama waktu tersebut ?
Pembahasan :
v0 = 2 m/s
v = 10 m/s
t = 8 s
Dijawab :
x = (v + v0) x 1/2 t
x = ( 10 m/s + 2 m/s ) x (1/2 x 8 s)
x = 12 m/s x 4 s
x = 48 m
9. Sebuah mobil mempunyai kecepatan awal 3 m/s. Ketika perpindahannya bertambah sebesar 10 m, maka kecepatannya menjadi 5 m/s. Berapakah percepatan mobil tersebut ?
Pembahasan :
v0 = 3 m/s
x = 10 m
v = 5 m/s
Dijawab :
v2 = v02 + 2 ax
52 = 32 + (2 x a x 10)
25 = 9 + 20 a
20 a = 25 – 9
a = 16/20
a = 0,8 m/s2
10. Sebuah pesawat mendarat dengan kecepatan 150 m/s. Mengerem sampai berhenti dalam waktu 20 sekon. Berapakah percepatan dan jarak tempuhnya ?
Pembahasan :
v = 0
v0 = 150 m/s
t = 20 s
Dijawab :
v = v0 + a t
0 = 150 m/s + (a x 20)
0 = 150 + 20a
-150 = 20a
a = -150/20
a= – 7,5 m/s2
Tanda negatif menunjukkan bahwa percepatannya diperlambat.
Jadi, jarak yang ditempuh dalam perpindahannya adalah :
v2= v02 + 2a ∆x
02 = (1502) + 2 (-7,5) ∆x
0 = 22.500 – 15 ∆x
15 ∆x = 22.500
∆x = 22.500/15
∆x = 1.500 m
Sekian pembahasan kali ini mengenai rumus GLBB dan GLB beserta contoh soal dan penjelasannya. Semoga bermanfaat!
When you login first time using a Social Login button, we collect your account public profile information shared by Social Login provider, based on your privacy settings. We also get your email address to automatically create an account for you in our website. Once your account is created, you'll be logged-in to this account.
DisagreeAgree
Connect withD
I allow to create an account
When you login first time using a Social Login button, we collect your account public profile information shared by Social Login provider, based on your privacy settings. We also get your email address to automatically create an account for you in our website. Once your account is created, you'll be logged-in to this account.
